데이터를 가져오고 추가하고 수정하고 없애고 하는 과정도 중요하지만, Dataframe으로 데이터의 분포와 경향성을 보는 것은 어디까지 한계가 존재한다. 이 데이터를 바탕으로 보기 좋게 시각화를 한다면 경향성이나 이상치, 결측치 등을 확인하기 편할 것이다.
matplotlib
말 그대로 수학 그림을 그리는 파이썬 라이브러리이다. 뒤에서 살펴볼 seaborn 또한 matplotlib에 기반을 두므로 시각화를 처음 접할 때 먼저 실습해 보기 좋은 라이브러리다. 근데 결국은 seaborn을 사용하는 게 편리하긴 하다.
seaborn
matplotlib을 추상화하여 작동하는 라이브러리이므로 사용이 간편하고 좀 더 예쁜 그림들을 쉽게 그릴 수 있으나 미세한 조정에는 결국에 matplotlib을 조금 사용해줘야 한다. 보통 두 라이브러리를 같이 쓰는 추세이나, 이 라이브러리가 계속 업데이트되고 있으니 결국에 표준으로 자리 잡을 수도 있겠다 싶다.
라이브러리 호출
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
삼각함수 그래프 그리기 1
x = np.arange(0,10,0.001)
y = np.sin(x)
z = np.cos(x)
plt.figure(figsize= (8,4))
plt.plot(x, y, label= 'sin(x)')
plt.plot(x, z, label= 'cos(x)')
plt.title('THIS IS LINE CHART')
plt.xlabel('X values')
plt.ylabel('Y values')
plt.legend()
plt.show()
첫번째 방식은 절차적(procedural) 방식의 시각화 코드이다. 그래프 위에 점을 찍을 건데, 이를 위해 정의역(x)과 사인(y), 코사인(z) 함수를 선언하였다. 그 뒤로는 plt의 속성을 정해주는 과정이다. 크기, 곡선, 제목, x/y축 라벨과 legend를 달아주고, show() 메서드를 통해 화면에 출력할 수 있다.
삼각함수 그래프 그리기 2
x = np.arange(0,10,0.001)
y = np.sin(x)
z = np.cos(x)
fig, ax = plt.subplots() # fig는 Figure, ax는 Axes 객체
fig.set_size_inches(8,4) # Figure 크기 설정
ax.plot(x, y, label= 'sin(x)')
ax.plot(x, z, label= 'cos(x)')
ax.set_xlabel('X values')
ax.set_ylabel('Y values')
ax.legend()
두번째 방식은 객체 지향적(OOP) 방식의 시각화 코드이다. fig와 ax는 각각 plt subplot의 그림 부분과 축 부분을 담당하는 객체가 된다. 그림의 사이즈를 정하고, 이어서 축 부분의 라벨과 legend를 달아준다. 여러 그래프를 다뤄야 할 경우에는 객체 지향적 방식이 좀 더 정교한 제어가 가능하고 복잡한 시각화 작업을 할 때 권장된다.

Scatterplot
x = np.random.rand(30)
y = np.random.randint(0, 30, 30) # 0부터 30까지의 수 중 랜덤으로 30개를 추출
z = np.random.randint(0, 30, 30)
plt.scatter(x, y, marker= "*", color= 'r', s= 100)
plt.scatter(x, z)
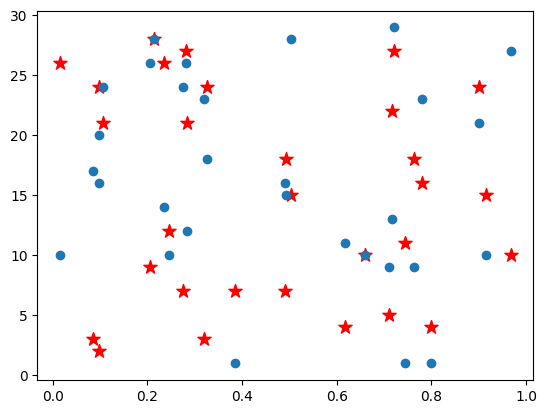
이어서 산점도이다. 2차원에서 어느 부분에 몰려있는지 보기에 편리하다. K-means나 KNN 같은 클러스터링 알고리즘을 수행할 때 많이 시각화하는 방식이다. 해당 코드에서는 0과 1 사이의 30개의 x좌표와, 이에 대응하는 0과 30 사이의 30개의 랜덤 수를 중복을 허용하여 추출하였다. 만약 중복 없는 난수를 원하면 np.random.choice()를 사용하면 되겠다.
z = np.random.choice(np.arange(0, 30), size=30, replace=False)
marker와 color로 점의 모양과 색상을 선택할 수 있고 s로 marker의 크기를 설정할 수 있다.
historgram
x = np.random.randn(100000)
plt.hist(x, bins=20)
이어서 히스토그램이다. 히스토그램은 해당 구간에 해당하는 데이터의 개수를 막대 형식의 그래프로 표현한 것이다. 기존의 막대 그래프와는 달리 x가 범위로 주어져 있다는 것이 차이점이다. 예시 코드는 정규분포를 따르는 100,000개의 샘플을 생성한 것이다. 해당 데이터가 존재할 수 있는 범위를 20개의 일정한 구간으로 나누어 표시하였다.

barplot
x = ['a', 'b', 'c', 'd']
y = [1, 5, 2, 8]
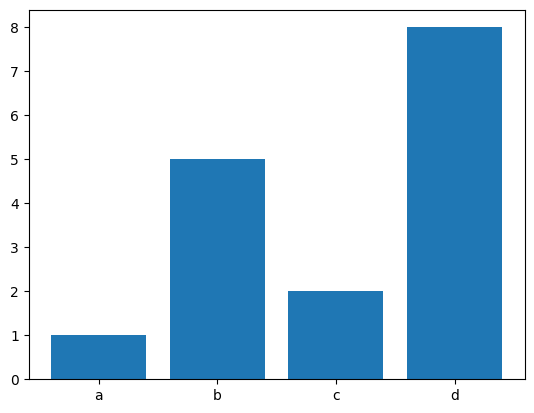
plt.bar(x,y)
그냥 단순하다. 알아서 보고 이해하길 바란다.
boxplot
i1 = np.random.normal(0, 2, 1000)
i2 = np.random.normal(-3, 1.5, 500)
i3 = np.random.normal(1.2, 1.5, 1500)
plt.boxplot([i1, i2, i3])
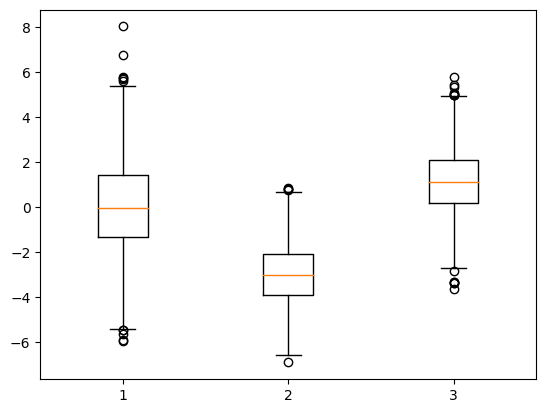
이어서 박스 플롯이다. normal() 메서드는 평균, 표준편차, 그리고 표본의 개수를 파라미터로 입력한다. 박스 플롯은 아마 EDA를 할 때 이상치를 체크하는 데에 있어서 가장 효과적인 시각화 그래프가 될 것이다. 하지만 박스 플롯으로 나타냈을 때 표시되는 그래프를 이해하기 위해서는 어느 정도의 사전지식이 필요하다.
Median
먼저 주황선은 중간값(Median)을 의미한다. 전체 데이터 중에 가장 가운데 값을 의미한다.
Box
주황선을 감싸는 box의 위 모서리는 전체 데이터의 75% 선이다. 이를 세 번째 사분위수라고 하며, 이 아래로 전체 데이터의 3/4이 표함 되어 있다는 뜻이다. 이어서 box의 아래 모서리는 전체 데이터의 25% 선이다. 이를 첫 번째 사분위수라고 하며, 이 아래로 전체 데이터의 1/4이 포함되어 있다.
Whiskers
box로부터 위아래로 길게 뻗어 가다가 어느 순간 멈추고 수평 선분이 표시된다. 이 지점은 box의 높이(세 번째 사분위수 - 첫 번째 사분위수)의 1.5배가 되는 지점이다. 데이터에서 말하는 최댓값과 최솟값이 되는 지점이 바로 여기인데, 여기를 한계로 지정하는 이유는 경향성에서 너무 벗어난, 즉 이상치(outlier)가 되는 데이터들을 제거해 주기 위함이다.
Outliers
Whisker를 벗어나 o로 표시된 데이터들을 의미한다. 경향성에서 너무 벗어나기 때문에 데이터에서 전처리할 때 제거할 가능성이 높다.
여러 개의 plot 그리기
이제 여러 그래프를 한번에 그려보자. 앞서 설명한 절차형 방식과 객체 지향형 방식을 둘 다 알아보자.
x = np.linspace(0, 10, 30) # 0부터 10까지의 구간을 30개로 자르겠다는 소리.
y = np.sin(x)
z = np.cos(x)
w = np.tan(x)
먼저 0부터 10까지의 구간을 균일한 30개의 구간으로 나누어 x의 값이 된다. 구간을 정하면 간격이 정해지는 방식을 원하면 linspace를, 간격을 정하면 구간의 개수가 정해지는 방식을 원하면 arrange를 사용하면 된다. 이어서 y, z, 그리고 w는 세 삼각함수의 그래프가 된다.
plt.figure(figsize= (12,5))
plt.subplot(2,2,1)
plt.plot(x, y, 'r-')
plt.subplot(2,2,2)
plt.plot(x, z, 'g-')
plt.subplot(2,2,3)
plt.plot(x, w, 'b-')
첫 번째 방식이다. figure의 크기를 정해주고 2 X 2로 나눠준 후, 각 위치에 차례대로 그려 넣는 방식이다. 직관적이지만, 순서가 엉키거나 값을 잘못 입력하면 에러가 발생할 수 있다.
fig, axes = plt.subplots(2,2)
fig.set_size_inches(12,5)
axes[0,0].plot(x, y, 'r-')
axes[0,1].plot(x, z, 'g-')
axes[1,0].plot(x, w, 'b-')
두 번째 방식이다. 먼저 객체를 선언하고 fig과 axes가 따로 속성을 정의한다. 차이점은 객체 지향 방식에서는 미리 2 X 2 배열을 그리기 때문에 총 3개의 그래프만 그려도 4번째 위치에 축이 그려져 있다는 점이다.

'AI' 카테고리의 다른 글
| [LLM] OpenAI API (3) - 파이썬 코드로 호출해 보기 (2) | 2024.11.02 |
|---|---|
| [LLM] OpenAI API (2) - Playground를 사용해 보자 (1) | 2024.11.01 |
| [LLM] OpenAI API (1) - API key 발급하기 (0) | 2024.10.30 |
| [LLM] 트랜스포머 구조 파헤치기 (1) - 텍스트를 임베딩 (Embedding)으로 변환하기 (3) | 2024.10.24 |
| [EDA] 탐색적 데이터 분석 with Python (1) (6) | 2024.09.25 |