Subproblem graphs
DP에서 우리는 sub-problem이 어떻게 구성되어 있는지, 그리고 서로 어떤 연관을 지니고 있는지를 이해하는 것이 중요하다.

위 그래프 중 오른쪽은 앞선 dynamic programming 1 포스팅에서 살펴봤었던 그래프이다. 해당 그래프는 4라는 문제를 해결하기 위해 어떤 sub-problem이 필요하고, 또 이들은 또 다른 sub-problem을 지니고 있음을 가시적으로 보여준다. 왼쪽 그래프는 오른쪽을 단순화한 버전이다.
우리는 subproblem graphs를 통해 어떤 문제를 해결할 때 필요한 sub-problem이 뭔지를 한눈에 알 수 있다. 궁극적으로는 이 그래프를 통해 시간 복잡도를 결정할 수 있는데, 실행 시간은 각각의 sub-problem을 해결하기 위한 시간의 합을 뜻하고, 각 sub-problem의 실행 시간은 해당 vertex의 차수의 개수에 비례한다.
Reconstructing solutions
DP를 통해 최적화된 정답뿐만 아니라, 그 정답을 도출해 내기 위한 과정 (solution) 또한 알고 싶다면 어떻게 해야 할까? 간단하다. sub-problem을 해결하는 과정을 배열에 저장해 주면 된다.

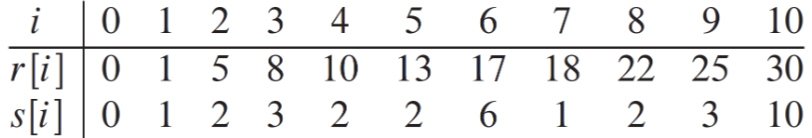

위 과정을 통해 나온 결과는 위와 같다. i = 7 일 때, 최댓값은 18이 나오는데 이는 어떤 sub-problem으로 이루어져 있을까? 의사 코드에 따라서 $PRINT-CUT-ROD-SOLUTION(p, 7)$ 을 계산해 보자.
$$
\begin{aligned}
s[7] &= 1 \; // \; print \; 1 \\
next &= 7 - s[7] = 6 \\
s[6] &= 6 \; // \; print \; 6 \\
next &= 6 - s[6] = 0 \; // \; terminate \\
So, \; r[1] + r[6] &= 1 + 17 = 18
\end{aligned}
$$
Elements of dynamic programming
그렇다면 언제 도대체 DP를 적용할 수 있을까? 사실 문제를 보고 어떤 방식으로 풀어야 할지 알아보는 건 매우 까다로운 일이지만 정답은 있다.
1. Optimal substructure
2. Overlapping subproblems
어떤 문제의 최적화된 솔루션이 여러 최적화된 sub-problem의 솔루션으로 이루어져 있고, 그네들이 여러 번 반복될 때 DP를 사용해 주면 된다.
Running time
그렇다면 rod-cutting example의 시간 복잡도는 어떻게 될까? 앞서 말했듯이 이 문제의 subproblem graphs를 확인해 주면 된다. 총 n개의 vertices (sub-problems)가 존재하고, 각 sub-problem은 최대 n - 1개의 또 다른 sub-problems (# of degrees; # of edges)를 봐야 하므로, 근사적으로 $O(n^{2})$의 시간 복잡도를 가진다.
'Computer Science and Engineering > Data Structures and Algorithms' 카테고리의 다른 글
| [Algorithm] NP-completeness (0) | 2024.05.26 |
|---|---|
| [Algorithm] Greedy (0) | 2024.05.20 |
| [Algorithm] Dynamic Programming 1 (0) | 2024.05.17 |
| [Algorithm] Binary Search Tree (0) | 2024.05.14 |
| [Algorithm] Sorting (Quick sort) (0) | 2024.04.21 |