Binary search tree
Search Tree 데이터 구조는 다음과 같은 operations를 제공한다.
- Search : 탐색
- Minimum : 최솟값
- Maximum : 최댓값
- Predecessor : 다음에 오는 요소
- Successor : 이전 요소
- Insert : 삽입
- Delete : 삭제
이와 같은 operations들은 트리의 깊이에 실행 시간이 비례한다. 완벽한 binary tree를 이룰 때에는 $\Theta(\lg(n))$ 의 시간 복잡도를, 만약 한쪽으로 치우쳐져 linear chain에 가깝다면 $\Theta(n)$의 시간 복잡도를 가지게 된다.
What is a binary search tree?
그렇다면 이분 탐색 트리란 무엇일까? 이분 탐색은 이분 트리의 모양으로, 각각의 node (object)끼리 linked data structure로 표현되는 녀석이다.
node라는 객체는 left, right, p (parent)로 또 다른 node를 가리킬 수 있게 구성된다. 만약 이러한 값들이 없다면 $NIL$로 표현될 수 있는데, 부모가 없는 유일한 노드는 루트 노드뿐이다.
이분 탐색 트리는 한 가지 중요한 특징이 있다. 바로 자신의 왼쪽 자식 트리는 자식보다 작아야 하고, 자신의 오른쪽 자식 트리는 자신보다 커야 한다는 것이다.
$$ x.left.key <= x.key <= x.right.key $$
탐색의 방식은 preorder, inorder, postorder 세 가지가 있으며, 어떤 노드부터 먼저 방문하는지에 따라 순회의 종류가 달라진다.
def preorder_tree_walk(x):
if x != None:
print(x.key)
preorder_tree_walk(x.left)
preorder_tree_walk(x.right)
위 코드는 전위 순회일 때 방문하는 알고리즘 의사코드이다. 전위 순회의 경우 부모 -> 왼쪽 자식 -> 오른쪽 자식의 방식으로 순회하기 때문에 다음과 같고, 중위 순회와 후위 순회에서는 현재 노드의 키 값을 언제 출력해 줄지만 변경해 주면 된다. 순회는 결국에 모든 노드를 한 번씩 방문하는 것이므로 $\Theta(n)$의 시간 복잡도를 가지게 된다.
Querying a binary search tree
앞서 살펴보았던 operation 중에 search, minimum, maximum, successor, 그리고 predecessor는 모두 $O(h)$의 시간 복잡도를 가진다.

그중 search부터 알아보자. search의 경우 재귀적으로도, 반복문으로도 구현이 가능하다. 결국에 원하는 요소를 찾기 위해 왼쪽/오른쪽 자식 노드로 향한다는 것은 탐색해야 할 요소의 개수가 반씩 줄어드는 것을 의미하므로 트리의 깊이만큼의 시간 복잡도가 필요하다.

minimum과 maximum은 상대적으로 구현이 아주 간단한데, 그도 그럴 것이 주어진 노드에서부터 왼쪽 자식 노드로 계속 이동하거나, 아니면 오른쪽 자식 노드로 계속 이동하기만 하면 되기 때문이다. 주의할 점은 파라미터에 들어가는 노드가 루트 노드가 되는 서브 트리에서의 최댓값과 최솟값을 반환한다는 것이다. 이 말은 즉슨, 전체 트리에 해당하는 최대/최솟값을 반환하는 것이 아니라는 것.
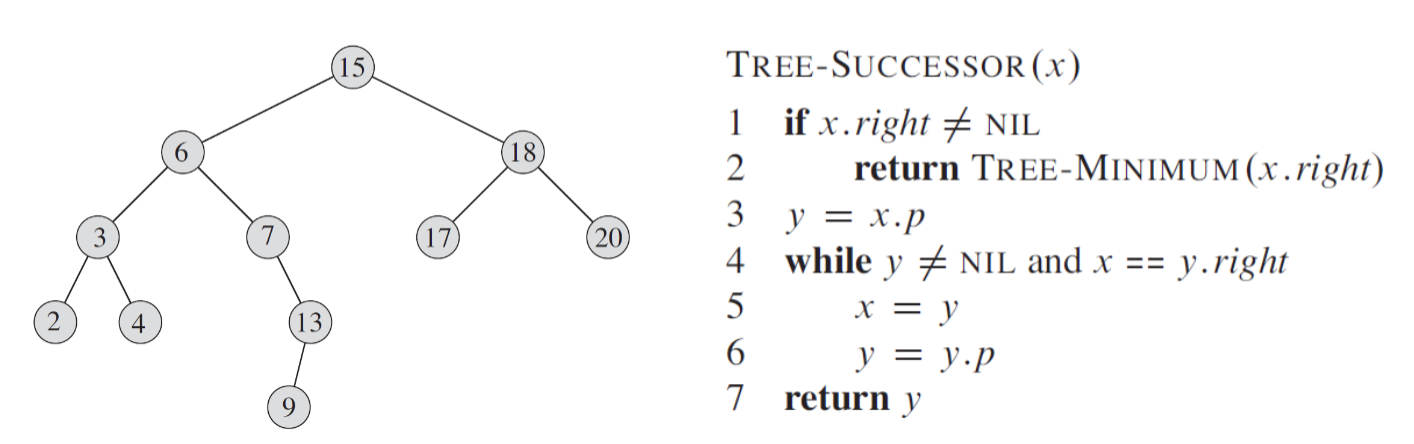
successor와 predecessor는 단순히 주어진 노드의 왼쪽과 오른쪽만을 의미하지 않는다. 만약 그런 노드가 없는 경우에도 우리는 이전 혹은 다음 노드를 찾아야 하므로, 트리를 좀 더 타고 올라가 다른 곳으로 파생되는 트리로 다시 접근해야 할 것이다. 주어진 트리 그림에서 9의 다음 녀석은 9의 오른쪽 자식 노드가 없기 때문에 오른쪽 자식 노드가 있는 노드인 15까지 올라가게 되고, 이때 15를 반환하게 되는 것이다. predecessor도 마찬가지의 방식으로 작동한다.
Insertion, Deletion
위 query들과 삽입/삭제를 따로 분리한 것은 예상했겠지만 이 두 operation의 구현이 매우 복잡하기 때문이다. 그럼에도 차근차근 살펴보자.

그래도 삽입은 나름 쉬운 편이다. T라는 트리에 z라는 요소를 삽입하려고 한다. 7번째 줄까지는 z가 들어갈 수 있는 적절한 위치를 찾는 과정이다. 다 찾고 나면 z의 부모를 y로 설정해 준다. 만약 z의 부모인 y가 $NIL$이라면 트리가 비어있다는 뜻이므로, 곧바로 z가 루트 노드가 된다. 나머지 경우에서는 z의 키 값과 y의 키 값 대소 비교를 통해 어느 위치에 둘 지를 결정한다.

삭제를 구현하기에 앞서, 미리 구현해 두면 좋은 transplant함수를 알아보자. 이 함수의 목적은 u를 루트 노드로 하는 서브 트리를 통째로 v를 루트 노드로 하는 서브 트리로 바꾸는 것이다. 코드를 살펴보면, u의 부모가 없을 경우 이는 u가 전체 트리의 루트 노드에 해당되므로 곧바로 전체 트리의 루트 노드를 v로 바꿔준다. 만약 u가 u의 부모 노드의 왼쪽에 위치한다면 v도 그 자리에 위치해야 하고, 만약 오른쪽에 위치한다면 v도 그 자리에 위치해야 한다. 마지막으로 u의 부모를 v의 부모로 설정한다.

이제 삭제를 위한 본 함수를 살펴보자. 사실 삭제의 경우 크게 4가지 경우에 따라 작동 방식이 다르기 때문에 자세히 살펴보면 좋겠지만, 현재 의사 코드로도 충분히 이해가 가능할 거라 믿는다. z라는 요소를 삭제하려고 할 때 1) z의 왼쪽 자식 노드가 없다면 z의 위치에 z의 오른쪽 서브 트리를 붙이면 된다. 이때 앞서 구현했던 transplant 함수를 사용하면 쉽다. 이어서 2) 오른쪽 자식 노드가 없다면 z의 위치에 z의 왼쪽 서브 트리를 붙이면 된다.
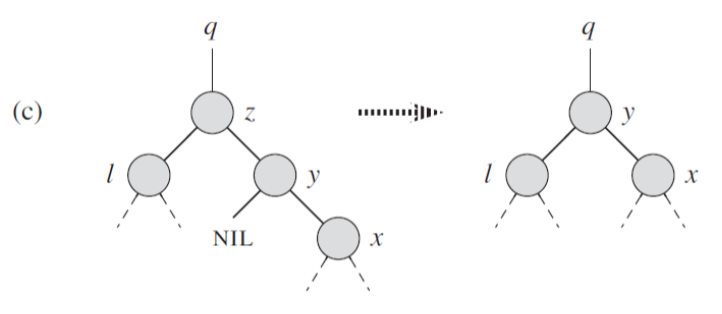
마지막으로 3) 둘 다 존재한다면 우리는 z의 successor가 필요하다. 이때에는 단순히 z의 오른쪽 서브 트리의 최솟값을 찾아주면 된다. 이렇게 찾은 y는 먼저 y가 바로 z의 자식인지를 판단해야 한다. y는 왼쪽 서브 트리가 없으므로 만약 바로 z의 자식이라면 transplant함수를 통해 접합만 시켜주면 된다. 위 그림은 그러한 y를 z의 위치에 접합시키는 과정이며, 의사 코드의 10 - 12번째 줄에 해당한다.

그런데 만약 y가 바로 z의 자식이 아니라면 문제는 조금 더 복잡해진다. 이럴 경우에는 y를 그냥 올려줄 수 없으므로 y의 오른쪽 자식 노드를 y의 위치에, 이어서 y는 z의 위치를 차지하기 위해 z의 오른쪽 자식 노드를 자신의 오른쪽 자식 노드로 만들고, 이 녀석의 부모도 자기 자신으로 만들어버린다.
'Computer Science and Engineering > Data Structures and Algorithms' 카테고리의 다른 글
| [Algorithm] Dynamic Programming 2 (0) | 2024.05.17 |
|---|---|
| [Algorithm] Dynamic Programming 1 (0) | 2024.05.17 |
| [Algorithm] Sorting (Quick sort) (0) | 2024.04.21 |
| [Algorithm] Sorting (Heap sort) (0) | 2024.04.08 |
| [Algorithm] Divide and conquer - Maximum Subarray (0) | 2024.04.03 |